นิยามของสมการพาราโบลา
พาราโบลา คือเซตของจุดบนพื้นระนาบซึ่งมีระยะห่างจากจุดคงที่ เท่ากับระยะที่ห่างจากเส้นคงที่
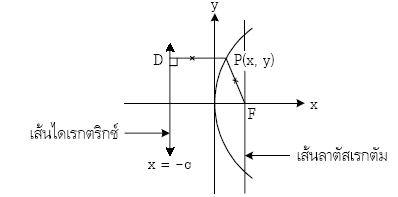
จุดคงที่ คือจุดโฟกัส (Focus)
เส้นตรงที่คงที่ คือเส้นไดเรกตริกซ์ (Directrix)
เส้นลาตัสเลกตัม (Latus Rectum) คือเส้นตรงที่ลากผ่านจุดโฟกัสและตั้งฉากกับแกนของรูป
แกนของรูปหรือแกนสมมาตร คือเส้นตรงที่ลากผ่านจุดยอดและผ่านจุดโฟกัส
คอร์ดของพาราโบลา คือเส้นตรงที่ลากเชื่อมจุด 2 จุด ที่ต่างกันของพาราโบลาและคอร์ดที่ลากผ่านจุดโฟกัสเรียกว่า Focul ส่วนคอร์ดที่ลากผ่านจุดโฟกัสด้วย และตั้งฉากกับแกนของรูปด้วย เรียกว่า ลาตัสเรกตัม(Latus Recrum)
ข้อสังเกตุ
จากสมการ จะต้องมีตัวแปรใดตัวแปรหนึ่งอยู่ในรูปกำลังสอง และอีกตัวหนึ่งยกกำลังหนึ่ง และอยู่ที่เทอมที่บวกลบกัน กราฟที่ได้จึงจะเป็นกราฟพาราโบลา
รูปแบบของพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)
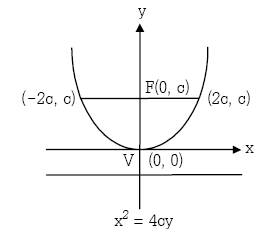พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน y
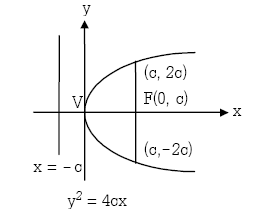พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน xเราสามารถสรุปสมการพาราโบลาออกมาได้ดังนี้
ไม่มีความคิดเห็น:
แสดงความคิดเห็น